今天,我们来研究这个:
于是乎,很多对GH有一定了解的朋友一定会说:“小菜一碟”
没错,这是一盘小菜,不过有好多碟,好多种思路,挺有趣的一道数学题。
作者收集几位同学的思路与大家一同分享,同时希望能拓宽同学们的思路,欢迎大家分享你们的想法!
在此之前,我们先弄清楚Divide Surface这个运算器(就这个: )
)
注意我们输入的UV值,反应的是对面“分成多少块”,与UV方向上的点数是X+1的关系
好啦,感受一下就是啦~自己试试就知道啦~~
思路一:递减
1,我们来观察一下当UV数值相差1及相等时的数据特点:
且不要管这一连串的算法,我们将面按U=5,V=4分割好,并把获取到的点反转一下再压扁(反转与否由你决定),得到这么面上这么一组数据
2,我们可以发现从0端开始的对角位置开始,往左右两个方向前进,这些连线的连接点数是在递减的,
3,在这个思路下,我们可以将左右两边筛选出来进行各自单独的连线:
(Divide Surface输入端的UV是分别附加了X-1,Series星端中除了左下角两个是X-1,外其余星端都是X+1)
都怪小编截图没作好—_—!大家实际操作一下,其实就懂了~
4,我们可以看到Polyline这个运算器是橙色的,说明有问题,问题很简单就是有一些组里只有一个点,运算后是nuLL空集。
与此同时,这种思路是有局限性的,当UV不相等且相差大于1时,会出现错误(图中白色箭头处,出现了两条连接点相同的线),
递减的思路在这里就不可以实现了,随着UV间距离拉大,这种相同连接点的线将随之增加
5,也就是这种算法是有局限性的,但是算法并无好坏,每一种思路都有其存在的合理性,或许在另外一个算法中起到关键作用
思路二:偏移
1,大家是不是觉得上面的案例有点像广州塔,我们就试试看呗
2,同样是看数据,不看算法。好吧,相信大家看出端倪了,我们想作的偏移实际与广州塔的偏移是有差别的,这里的偏移是01010……(会懂的),广州塔的偏移是11111且并不舍弃数据的,我们作了舍弃数据的作法在后面连线时就不能按广州塔的作法,舍弃数据对数据结构的破坏对我们接下来进行操作带来不少的麻烦,但是我们从这里也可以看出封闭面与开放面在数据处理的那细微又巨大的不同
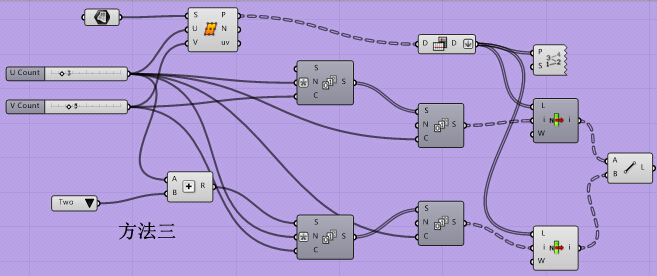
思路三:单纯的点对点连接
1,一个本来看起来简答的东西被我们这么一折腾好像又变复杂了,然而简单往往是一个算法制胜的关键。那么,我们就先静下心来,观察一下
这当中的数据特点。我们以单纯的“点对点”连接思路看,我们需要作的仅仅是将点筛选成两组,然后点对点连线
2,筛选出这么两组点
3,最后,连线。没错结束啦(星号都是X+1)
4,这是针对开放面,斜向连线,较佳的算法,回归到数据本身,同时纯粹的找点连线的思路清晰明朗