今天我们来学习Grasshopper的系列教程,今天要学习的内容是:Meta球
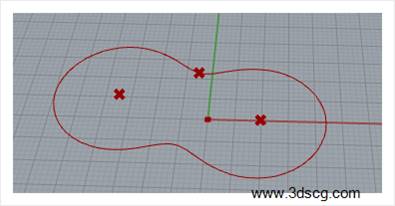
Meta球是用两个或者两个以上的点作为曲线的圆心,在圆的外侧设定一个点作为引力因子,使其能对圆形产生因引力引起的变化。
从另外一个角度去理解,我们也可以理解为两个小水滴挨得很近,他们也会互相吸引,那这两个小水滴没有完全融合之后的效果,就是Mate球了

MetaBall:Mate球
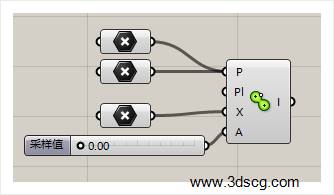
Grasshopper运算器左边的参数分别代表的是:
\1. 输入Mate球的圆心点,圆心点的数量要求是两个以上的。
\2. 输入Mate球参考平面
\3. 输入外部的引力因子
\4. 生成的曲线的采样值,如果参数等于0,输出的就是平滑的曲线,如果是大于0,输入多段线,这个数值就充当多段线每一个线段的长度。
MetaBall(t):通过曲线的曲率控制的Mate球
和上一个运算器的差别就是曲线是通过曲率值控制了,不是通过采样值控制的


MetaBall(t) Cus tom:更多参数的Mate球
这个可以单独控制每一个Mate球的圆心的引力大小,这里要注意的就是引力值的个数要和圆心点数量一致,否则会报错。


[stag_sidebar id=”gh-article”]
好的,我们今天课程就到这里,如果有其他关于Grasshopper的其他问题也可以在本节课下面的留言窗口留言,这样可以讨论关于Grasshopper的技术问题,我是LinkLi,下次课再见。
