今天我们来学习Grasshopper的系列教程,我们今天来学习,在曲线上做平面的方法。
在曲线上做平面,这类运算器和我们上节课讲的在划分曲线是差不多的,划分曲线是在曲线上做点,而今天我们的内容,是在曲线上做平面,点和平面既有相同点,也有不同点。
相同地方,不管是点还是平面,我们都可以看作点来操作。不同点之处的在于点是没有方向的,而平面它是有方向的,通常平面我们都可以拆分为xyz三个方向,而点只能拆分为xyz三个点坐标。
通过生成平面,我们可以为后续的操作做一些准备,比如我们要运动点,我们必须有方向,比如我们要绘制一条曲线,这条曲线它是有定向方向的,那我们必须有这个平面坐标,那这里的一切我们都可以生成平面开始,当然制作平面的方法那是多种多样的,也不单单是这种,只是说基于犀牛的建模原理,我们往往都是从曲线入手的,曲线才是犀牛的灵魂,参数化建模当然也不例外了。
Curve frames:做曲线上的等分平面
Horizontal frames:做曲线上的等分水平面
Perp frames:做和曲线垂直的等分平面
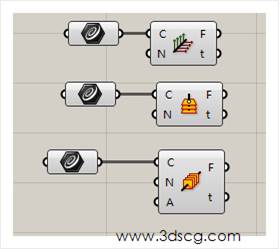
这三个运算器的用法都是差不多的,我这里把它拿到一起来讲,在上图中我们可以看到它的输入端口和输出端口的参数都是一样的,左边的n端口的是输入等份的数量,右边的f端口是输出等分的平面,t端口是等分平面在曲线上的位置参数,那我们就来看一看这三个究竟有什么区别。
我们先来看看第2个和第3个吧,这两个的区别比较大,第2个运算器是生成的是一个水平面,而第3个生成的是和曲线垂直的平面,这一点我们从第3个运算器的图标都能清晰的看出来。
接下来是第1个和第2个的区别。
这两个这两个生成的平面的都不是以曲线垂直的,第1个生成的平面会跟曲线所在点的位置成一个平面,这个怎么理解呢?请看下图,
我们可以在下面的图例当中可以看到沙僧人的平面都是倾斜的,那为什么会倾斜呢?因为这条曲线上的这个点就是倾斜的,

而第2个运算器则不是,大家可以看一下第2张图
我们可以看到生成的平面跟这个曲线,它在方向上并没有什么关联,这个平面它是跟xy平面是平行关系,这就是两者之间最大的差别

这三个运算器我们用Grasshopper做设计的时候也是经常用到的,至于选用哪个,我们得实际看曲线的造型,曲线的走向,跟我们的设计注重点来选择。
好的,我们今天课程就到这里,如果有其他关于Grasshopper的其他问题也可以在本节课下面的留言窗口留言,这样可以讨论关于Grasshopper的技术问题,我是LinkLi,下次课再见。
