今天我们来学习Grasshopper的系列教程,我们今天学习的是关于直线的绘制,我们在下面的学习中,可以学习到多种生成直线的方式
实现也是我们做参数化设计里的一个大的分支,建筑的很多造型还是由很多直线构成的,我们通通过构建直线也可以构建复杂的曲面,所以各位同学一定要好好掌握直线是怎么创建的,好了,那我们来开始今天的课程吧。
嗯嗯,
Fit Line:多个点拟合成直线
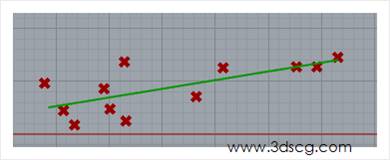
会一堆杂乱无章的点生成一条直线,这个运算器没有任何参数,只要输入点就可以了
点拟合成直线,请看下图
Line:2点生成直线
这个也是一个非常常用的运算器,只要输入ab两个点就可以了,非常简单。
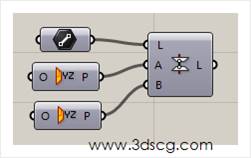
Line 2Plane:被两个平面截断的直线
使用这个运算器必须先准备一条直线,然后两个截断这条直线的平面,那么就可以得到两个平面之间的直线段了。
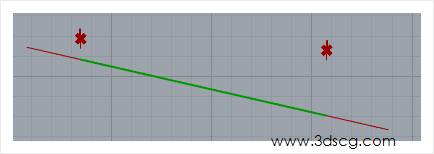
在下图中我们看到两个红点就是两个平面,两个红点的下方有一段绿色的线段,那个就是被截断之后的直线段,
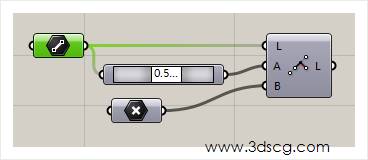
Line 4pt:利用4个点生成直线
这个运算器,其实并不用输入4个点,而是准备一条直线,和这条直线上的一个点,加上直线外的任意点,那么我们就能得到一条线段了。
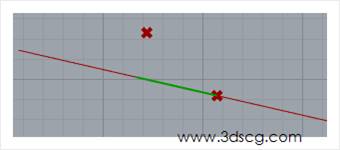
上面解释啊,可能有点复杂,但是我们结合下图的效果来看,我们会发现线外的点和线上的点还有直线,他们其实是组合成了一个直角三角形,而得到的线段就是在这条直线上的一个直线边。
这样下图的绿色线段。
Line SDL:Sdl直线
Sdl直线就是已知起始点,线的方向还有线的长度构成的一个直线段,算法比较简单,大家看下图的算法就可以了。
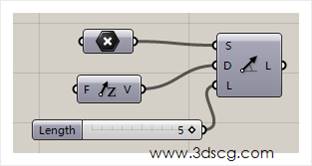
Tangent lines:切线直线
这个运算器用于计算圆外面的点到圆上面的两个切线段,T1和t2端口分别输出两个直线段
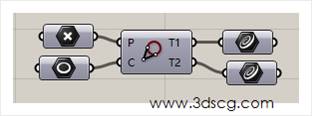
效果请看下图
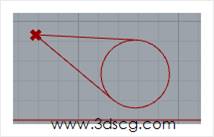
我们使用这个算法扩充一下,请看下图的算法。
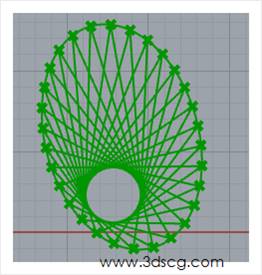
在下图开始阶段,我们绘制了一个椭圆曲线,然后把这个椭圆曲线进行30等份,然后把等份点输入到这个运算器里面去,我们就会得到一个交错的网架图
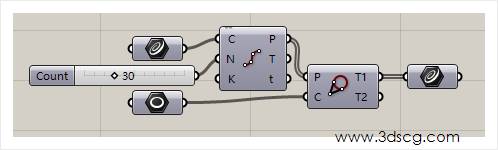
网架图的效果请看下图
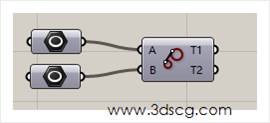
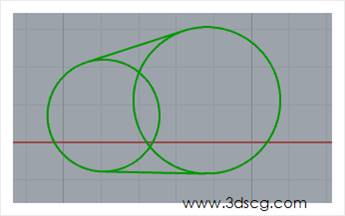
Tangent Lines (Ex):两个圆之间的切线段
这个运算器是上一个的增强版,需要用到两个圆
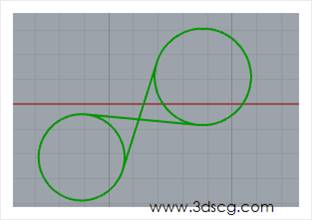
Tangent Lines(In):两个圆之间的切线段
这个产生的切线段是交错的,原理和上一个运算器基本上是一样的
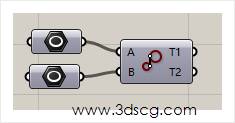
效果图请看下图
好的,我们今天课程就到这里,如果有其他关于Grasshopper的其他问题也可以在本节课下面的留言窗口留言,这样可以讨论关于Grasshopper的技术问题,我是LinkLi,下次课再见。
今天我们来学习Grasshopper的系列教程,我们今天学习的是关于直线的绘制,我们在下面的学习中,可以学习到多种生成直线的方式
实现也是我们做参数化设计里的一个大的分支,建筑的很多造型还是由很多直线构成的,我们通通过构建直线也可以构建复杂的曲面,所以各位同学一定要好好掌握直线是怎么创建的,好了,那我们来开始今天的课程吧。
嗯嗯,

Fit Line:多个点拟合成直线
会一堆杂乱无章的点生成一条直线,这个运算器没有任何参数,只要输入点就可以了

点拟合成直线,请看下图

Line:2点生成直线
这个也是一个非常常用的运算器,只要输入ab两个点就可以了,非常简单。

Line 2Plane:被两个平面截断的直线
使用这个运算器必须先准备一条直线,然后两个截断这条直线的平面,那么就可以得到两个平面之间的直线段了。

在下图中我们看到两个红点就是两个平面,两个红点的下方有一段绿色的线段,那个就是被截断之后的直线段,

Line 4pt:利用4个点生成直线
这个运算器,其实并不用输入4个点,而是准备一条直线,和这条直线上的一个点,加上直线外的任意点,那么我们就能得到一条线段了。

上面解释啊,可能有点复杂,但是我们结合下图的效果来看,我们会发现线外的点和线上的点还有直线,他们其实是组合成了一个直角三角形,而得到的线段就是在这条直线上的一个直线边。
这样下图的绿色线段。

Line SDL:Sdl直线
Sdl直线就是已知起始点,线的方向还有线的长度构成的一个直线段,算法比较简单,大家看下图的算法就可以了。

Tangent lines:切线直线
这个运算器用于计算圆外面的点到圆上面的两个切线段,T1和t2端口分别输出两个直线段

效果请看下图

我们使用这个算法扩充一下,请看下图的算法。
在下图开始阶段,我们绘制了一个椭圆曲线,然后把这个椭圆曲线进行30等份,然后把等份点输入到这个运算器里面去,我们就会得到一个交错的网架图

网架图的效果请看下图

Tangent Lines (Ex):两个圆之间的切线段
这个运算器是上一个的增强版,需要用到两个圆


Tangent Lines(In):两个圆之间的切线段
这个产生的切线段是交错的,原理和上一个运算器基本上是一样的

效果图请看下图

好的,我们今天课程就到这里,如果有其他关于Grasshopper的其他问题也可以在本节课下面的留言窗口留言,这样可以讨论关于Grasshopper的技术问题,我是LinkLi,下次课再见。
